Cách Tính Tích Phân Kép

Tích phân kép chủ yếu hèn được áp dụng để tìm diện tích bề mặt của hình 2d. Nó được thể hiện bằng ‘∫∫’. Chúng ta hoàn toàn có thể dễ dàng search thấy diện tích s của một vùng hình chữ nhật bởi tích phân kép. Nếu chúng ta biết tích phân đơn giản và dễ dàng thì sẽ dễ dàng giải được những bài toán tích phân kép. Vì vậy, trước hết, họ sẽ bàn bạc về một số trong những quy tắc cơ bản của tích hợp.Tích phân là 1 phần rất đặc biệt của giải tích. Có không ít kiểu tích hòa hợp như tích hợp 1-1 giản, tích vừa lòng kép, tích thích hợp ba. Chúng ta thường xuyên sử dụng phép tính tích phân để tìm diện tích và thể tích trên một phần trăm rất lớn, rất có thể được xác định bằng những công thức hoặc phép tính solo giản.

Bạn đang xem: Cách tính tích phân kép

Quy tắc tích phù hợp kép

Trong giải tích, bọn họ thường tuân theo các quy tắc và công thức để thực hiện bất kỳ phương pháp tích phân nào. Để giải những bài toán tích phân, bạn phải nghiên cứu nhiều phương thức khác nhau như tích phân theo cỗ phận , tích phân thay thế hoặc sử dụng công thức. Trong trường hòa hợp tích hợp kép cũng vậy, chúng ta sẽ bàn bạc ở trên đây quy tắc tích thích hợp kép theo các bộ phận, được giới thiệu bởi;

∫∫u dv / dx dx.dy = ∫ dy

Các nằm trong tính của Tích phân kép

Các đặc thù của tích phân kép như sau:

∫ x = a b ∫ y = c d f (x, y) dy.dx = ∫ y = c d ∫ x = a b f (x, y) dx.dy∫∫ (f (x, y) ± g (x, y)) da = ∫∫f (x, y) domain authority ± ∫∫g (x, y) dANếu f (x, y) k ∫∫f (x, y) .dA = ∫∫kf (x, y) .dA∫∫ R∪S f (x, y) .dA = ∫∫ R f (x, y) .dA + ∫∫ s f (x, y) .dA

Ngoài ra, hãy đọc:

Hội nhậpTích phân xác địnhTích hợp bằng cách thay thếQuy tắc tích hợpTích phân mang lại lớp 12

Diện tích tích phân đôi

Cho z = f (x, y) xác minh trên miền D trong mặt phẳng xy và bọn họ cần tra cứu tích phân kép của z. Nếu bọn họ chia vùng quan trọng thành những sọc dọc và cảnh giác tìm các điểm cuối mang đến x với y tức là các số lượng giới hạn của vùng, thì bạn cũng có thể sử dụng công thức;

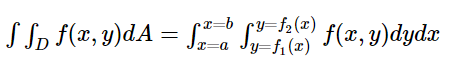
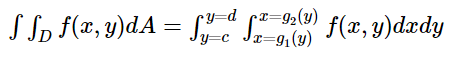
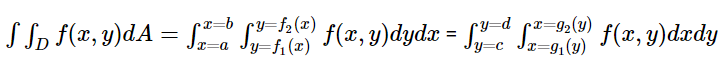
Trong các loại tích phân kép này, đầu tiên, bọn họ phải tích phân f (r, θ) so với r giữa những giới hạn r = r 1 và r = r 2 coi θ là hằng số cùng biểu thức kết quả được tích phân đối với θ từ bỏ θ 1 đến θ 2 . Ở trên đây r 1 và r 2 có thể là hằng số hoặc hàm của θ.

Trong trường hợp này, trước tiên, chúng ta phải tích phân f (r, θ) đối với θ giữa các giới hạn θ = θ 1 và θ = θ 2 và coi r như 1 hằng số và biểu thức kết quả được tích hợp so với r và điều đó thời gian hàm của θ sẽ không còn đổi.

Xem thêm: Mật Khẩu 4 Số Ý Nghĩa - Mật Mã Tình Yêu ⇒By Tiếng Trung Chinese

Ví dụ về Tích phân kép

Câu 1: Đánh giá ∬ (x 2 + y 2 ) dxdy

Giải: Giả sử, I = ∬ (x 2 + y 2 ) dxdy

I = ∫ <∫ (x 2 + y 2 ) dx> dy

I = ∫ dy

I = x 3 y / 3 + xy 3 /3

I = / 3

Câu 2: Giải hàm ∫∫x.logx.dx.dy

Giải pháp: Giả sử I = ∫∫x.logx.dx.dy

Đầu tiên, họ hãy lấy tích phân bên phía trong của những hàm ∫x.logx dx.

Bằng luật lệ tích phân theo cỗ phận, bạn cũng có thể giải được tích phân trên;

∫x.logx dx = ∫ (logx) x dx

Hàm logarit trên hàm x cùng với hàm x khác không được tích phân trực tiếp. Vì vậy, chúng ta cũng có thể coi nó là;

u = log x cùng dv = x dx

Vì vậy, du = (1 / x) dx.v = x 2 /2

Do đó, ∫x.logx.dx = (logx) x 2 /2 – ∫ (x 2 /2) (1 / x) dx

= x 2/2 (logx) −1/2 ∫x.dx

Do đó, ∫x.logx.dx = x 2 /2 (logx) – 1 / 4x 2

Đây là kết quả thu được dưới phép tích phân từng phần so với tích phân mặt trong. Bây giờ, hãy quản lý nó với các hàm tích phân phía bên ngoài bằng cách:

∫∫x.logx.dxdy = ∫ dy

I = ∫ dy – ∫ <1 / 4x 2 > dy

I = (x 2 y / 2) (log x) – 1 / 4x 2 y.dy + c

Câu 3: Giải ∬ (x + y) dxdy

Lời giải: Giả sử, I = ∬ (x + y) dxdy

I = ∫ <∫ (x + y) dx> dy

I = ∫ dy

I = x 2 y / 2 + xy 2 /2

I = (xy / 2) (x + y)

Câu 4: Giải ∬ (2x − 3y) dydx

Giải: Giả sử, I = ∬ (2x − 3y) dxdy

I = ∫ <∫ (2x − 3y) dx> dy